欧拉遇到过的最难的积分：全体自然数的立方倒数和

（本文原载于我在知乎上的回答，原问题是：“你遇到过的最难的积分题目是什么？”，略修改）

这不是我遇到过的最难的积分，这是欧拉遇到过的最难的积分：

1734年，27岁的欧拉计算出全体自然数的平方的倒数和是 :

这个成就使欧拉一下子名声大噪，成为数学家中的社会名人。以上这个问题后来以欧拉的家乡瑞士巴塞尔命名，称为“巴塞尔问题”。

欧拉自己也很兴奋，他一鼓作气，计算了指数为偶数，直到26次方的自然数幂次倒数和的情况：

…

那么问题就来了，指数为3的情况下，结果如何呢？这个问题意外地困难。欧拉一生中曾经多次挑战这个问题，找到了许多相关结果，比如奇数的3次幂的交错级数情况：

然而欧拉始终不能对自然数立方倒数和问题找出一个“简单”的确切答案。他曾经“自然地”（因为偶数幂次都是这个形式）作出猜想，这个问题的答案应该是: 的形式，其中是个有理数。

后来，他又找到了文章开头的那个积分式：

然而这个积分看似简单，但始终无法继续计算或化简。

1785年，在欧拉去世后2年出版的论文中，可以看到欧拉在生命中的最后岁月仍在尝试解决这个问题。欧拉写到“…迄今为止，没有任何办法写出这个级数的封闭形式…但是答案可能是这样一种形式”:

其中 和是有理数。

欧拉承认：“我用过如此多的方法寻找自然数的立方倒数和，然而所有方法均徒劳无功。以上（积分式）的方法也没有产生任何结果，所以看上去放弃（研究这个问题）是正确选择…”

近200年后，1978年，Roger Apery证明：全体自然数的立方倒数和是一个无理数。

他证明的结论并不让人吃惊，让数学家吃惊的是，对这个问题的研究居然还能产生一些进展，因为欧拉都放弃了！现在全体自然数的立方倒数和就被被称为“Apery常数”。

有人问对平方倒数和可否凑出类似的积分式？仿造欧拉的方法，很容易得到如下积分式，恰好等于全体自然数的平方倒数和：

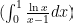
有wolframalpha为证：

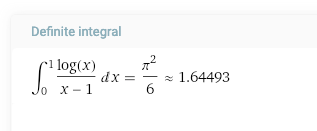
这个不定积分wolfram给我的答案是：

不是常见的封闭形式，而使用了对数积分函数。2021.12.8我收到知乎用户“诱宵美9”私信，她搞出一个可以积的，全体自然数平方倒数和的积分，计算过程如下：

用换元：

从而有：

交换积分级数顺序:

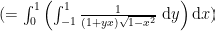
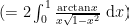
从而：

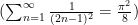
于是有：

牛，这个我是想不出来的！就是有点复杂，期待还有更简单形式的积分。

以下是目前有关此问题的一些进展：

首先如果把指数视为自变量，则以上级数求和已被一般化，归入黎曼Zeta函数(以下定义仅适用s>1的情况)：

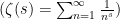
对于s为偶数的情况，欧拉时代就已经解决：

其中 称为“伯努利数”，它们满足递推关系：

对s为奇数的情况则所知甚少。1978年Apery证明 是无理数，仍未知其是否超越数。2001年有人证明，必然有无穷多个 是无理数，且 、 、 、中，至少有一个是无理数。

开头那个积分是欧拉算不出的，以下介绍一个欧拉遇到过的，也相当难但确实是可以算的积分：

不妨自己先算算看……

当代“规范”解法，先拆分：

再换元，令t=x/2：

原积分形式复现，太好了，可以解出:

.

欧拉的“不规范”解法：

首先，证明这样一个等式：

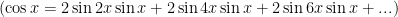
方法是，根据积化和差公式：

所以：

再计算的微分，当然， ,代入以上公式：

再倒回去，对两边积分：

C是一个待定的常数。恰好已知当 时， ，代入上式，可得：

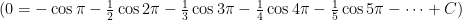
那么:

，恰好这个级数值是已知的(这道题大概很多课本里是作为习题的吧)，为 ，所以得到：

然后就可以求它的积分了：

以上过程中，每一项sin都正好抵消。

欧拉的方法虽然看上去很繁复，但有一种把无穷级数玩弄于股掌之间的感觉。